[Swift] 플로이드 워셜(Floyd-Warshall) 알고리즘 - 최단 경로 구하기
플로이드 워셜(Floyd-Warshall) 알고리즘
플로이드 워셜 알고리즘은 그래프에서 모든 노드 간의 최단 경로를 찾는 알고리즘이다. 이 알고리즘은 다익스트라(Dijkstra) 알고리즘과 유사하지만, 다익스트라 알고리즘이 하나의 출발점에서 모든 다른 노드까지의 최단 경로를 찾는 것과 달리, 플로이드 워셜 알고리즘은 모든 노드 쌍 간의 최단 경로를 찾는다. 어떻게 보면 다익스트라 알고리즘 보다 더 상위 기술로 보이지만 다익스트라 알고리즘이 더 우월한 시간 복잡도를 갖는다.
플로이드 워셜 알고리즘은 동적 계획법을 사용하여 구현된다. 알고리즘의 핵심은 "거쳐가는 노드"를 기준으로 최단 경로를 갱신하는 것이다. 알고리즘은 인접 행렬로 표현된 그래프를 입력으로 받는다. 그리고 i에서 j로 가는 최단 경로를 저장하는 2차원 배열을 초기화한다. 그리고 나서 알고리즘은 i에서 j로 가는 경로를 고려할 때, k를 거쳐가는 경로가 더 짧은지 확인한다.
플로이드 워셜의 기본 아이디어
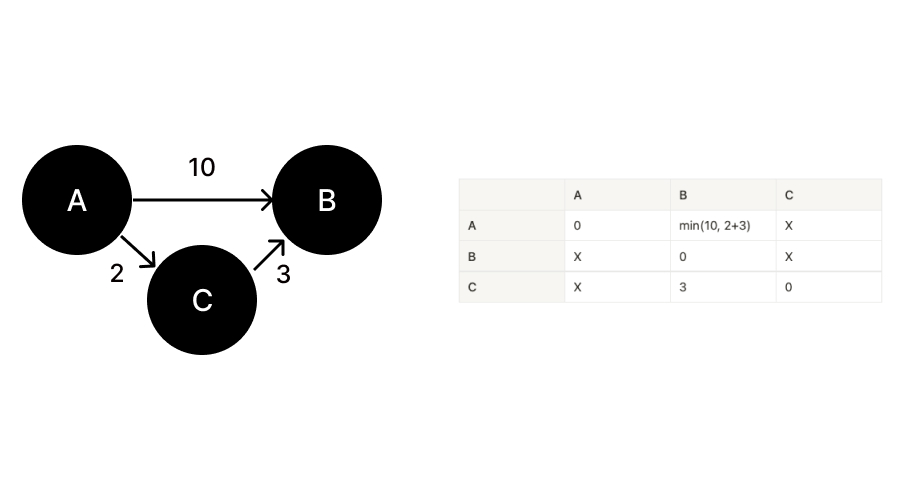
플로이드 워셜의 기본 아이디어는 “무언가 거쳐가는 것”과 “거쳐가지 않는 것”을 비교 하여 더 빠른 정보의 데이터를 테이블에 업데이트 하는 것이다. 당연히 상식상 무언가를 거쳐가는 것이 더 오래걸리는거 아니냐 생각할 수 있지만, 각 노드간의 거리가 다르기 때문에 거쳐가는 것이 더 빠를 수 있다. 위 이미지는 화살표 방향으로 노드에서 다른 노드간의 거리(간선)를 표시한 것이고 그 오른쪽 표는 최단 경로 표이다. 위 표와 같이 A에서 B로 가는 최단 거리는 바로가는 것(10)과 C를 거쳐 가는 것(2+3)을 비교해서 더 작은 수치로 나타낼 수 있다.
플로이드 워셜의 시간복잡도
알고리즘은 3중 반복문으로 구성되어 있다. 첫 번째 반복문은 거쳐가는 노드를 선택하는 k를 반복한다. 두 번째 반복문은 출발 노드를 선택하는 i를 순회한다. 세 번째 반복문은 도착 노드를 선택하는 j를 순회한다. 이 때, 각 반복문은 V번 순회하게 되므로, 전체적인 시간 복잡도는 O(V^3)이 된다.
다익스트라 vs 플로이드 워셜
다익스트라 알고리즘은 로그 선형 시간 복잡도(O(N*logM))가 소요된다. 플로이드 워셜에 비해 매우 빠른 알고리즘이다. 하지만 다익스트라는 다소 코드가 복잡하고, 🔗 힙(heap)자료구조를 사용하는데 Swift는 Heap 자료구조를 지원하지 않기 때문에 직접 heap을 구현해야 하여 코드 작성에 많은 시간이 소요된다.
만약 문제가 하나의 시작점에서 다른 경로를 탐색하는 알고리즘이라면 다익스트라 알고리즘을 사용하는 것이 좋지만, 각 간선(노드 사이 거리)중 음의 간선(음수값)이 있는 경우 다익스트라로 구현할 수 없으므로 플로이드 워셜 알고리즘을 활용해서 문제를 풀거나 다른 방식을 찾아야 한다.
Swift 코드로 플로이드 워셜 구현
swiftimport Foundation let graph: [[Int]] = [ [0, 4, Int.max, 6], [3, 0, 7, Int.max], [5, Int.max, 0, 4], [Int.max, Int.max, 2, 0] ] let numNodes: Int = 4 func floydWarshall(_ graph: [[Int]], _ numNodes: Int) -> [[Int]] { var dist = graph for k in 0..<numNodes { for i in 0..<numNodes { for j in 0..<numNodes { if i == j || i == k || j == k { continue } if dist[i][k] == Int.max || dist[k][j] == Int.max { continue } if dist[i][k] + dist[k][j] < dist[i][j] { dist[i][j] = dist[i][k] + dist[k][j] } } } } return dist } print(floydWarshall(graph, numNodes))
주어진 graph에서 Int.max는 문제에서 거리가 정의되지 않은 경우이고, 출발점과 끝점이 같은 경우이다. 위 코드를 실행하면 아래와 같은 결과 값을 얻을 수 있다.
swift[ [0, 4, 8, 6], [3, 0, 7, 9], [5, 9, 0, 4], [7, 11, 2, 0] ] Program ended with exit code: 0
기타 및 참고 자료
저작권 등 문제가 되는 부분이 있다면 삭제하겠습니다.