[번역] Constraint 톺아보기 (Anatomy of a Constraint) 1/2

작성일 : 2023-04-19

개요

해당 문서는 학습 목적으로 Apple 공식 문서인 🔗 Auto Layout Guide을 번역한 글입니다. 다소 오역이 있을 수 있어 잘못된 내용이 있을 수 있습니다. 문제가 되거나 오류가 있다면 댓글 부탁드립니다.

내용

View 계층 구조의 레이아웃은 일련의 선형 방정식으로 표현할 수 있습니다. 각 제약 조건(Constraint)은 단일 방정식으로 표시됩니다. 우리의 목표는 가능한 답이 하나뿐인 방정식을 선언하는 것입니다.

간단한 예로 방정식을 설명하겠습니다. 아래를 참고해주세요.

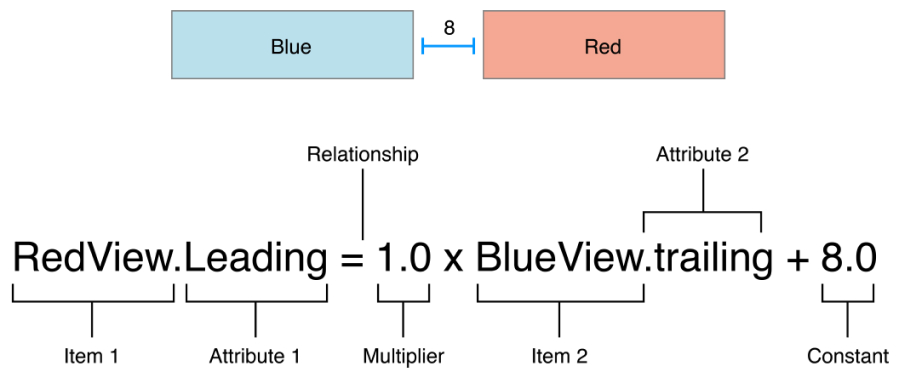
이 제약 조건은 Red View의 leading이 Blue View의 trailing 과의 8.0pt 떨어져 있어야한다고 표현하는 것입니다. 방정식에는 여러 부분이 있습니다.

item 1: 방정식의 첫 번째 항목(위의 경우 Red View). item은 반드시 View 또는 레이아웃 가이드여야 합니다.
attribute 1: 첫 번째 item의 제약을 받을 속성(위의 경우 RedView의 leading을 의미)
relationship: 좌변과 우변의 관계입니다. 관계는 같음 크거나 같음 또는 작거나 같음의 세 가지 값 중 하나를 가질 수 있습니다. 위의 경우 좌과 우변은 같습니다.
multiplier: attribute2의 값에 이 부동 소수점 숫자를 곱 합니다. 이 경우 승수는 1.0입니다.
Item 2: 방정식의 두 번째 항목(위의 경우 BlueView). 첫 번째 항목과 달리 비워 둘 수 있습니다.
attribute 2: 두 번째 항목에 제약을 받을 속성입니다(이 경우BlueView의 trailing). Item2가 비어 있는 속성은 존재하지 않습니다.
constant: 상수 부동 소수점 offset(이 경우 8.0)입니다. 이 값은 속성 Attribute 2의 값에 추가됩니다

대부분의 제약 조건은 사용자 인터페이스에서 두 항목 간의 관계를 정의합니다. 이러한 항목은 View 또는 레이아웃 가이드를 나타낼 수 있습니다. 제약 조건은 항목의 높이와 너비 사이의 종횡비를 설정하는 것과 같이 단일 항목의 서로 다른 두 속성 간의 관계를 정의할 수도 있습니다. 항목의 높이나 너비에 상수 값을 할당할 수도 있습니다. 상수 값으로 작업할 때 두 번째 항목은 비워두고 두 번째 특성(Attribute 2)은 Not An Attribute로 설정되며 multiplier는 0.0으로 설정됩니다.

오토 레이아웃 속성(Auto Layout Attributes)

오토 레이아웃에서 속성은 제한할 수 있는 기능을 정의합니다. 일반적으로 여기에는 4개의 가장자리(leading, trailing, top 및 bottom)와 높이, 너비, 수직 및 수평 중심이 포함됩니다. 텍스트 항목에는 하나 이상의 기본 속성도 있습니다.

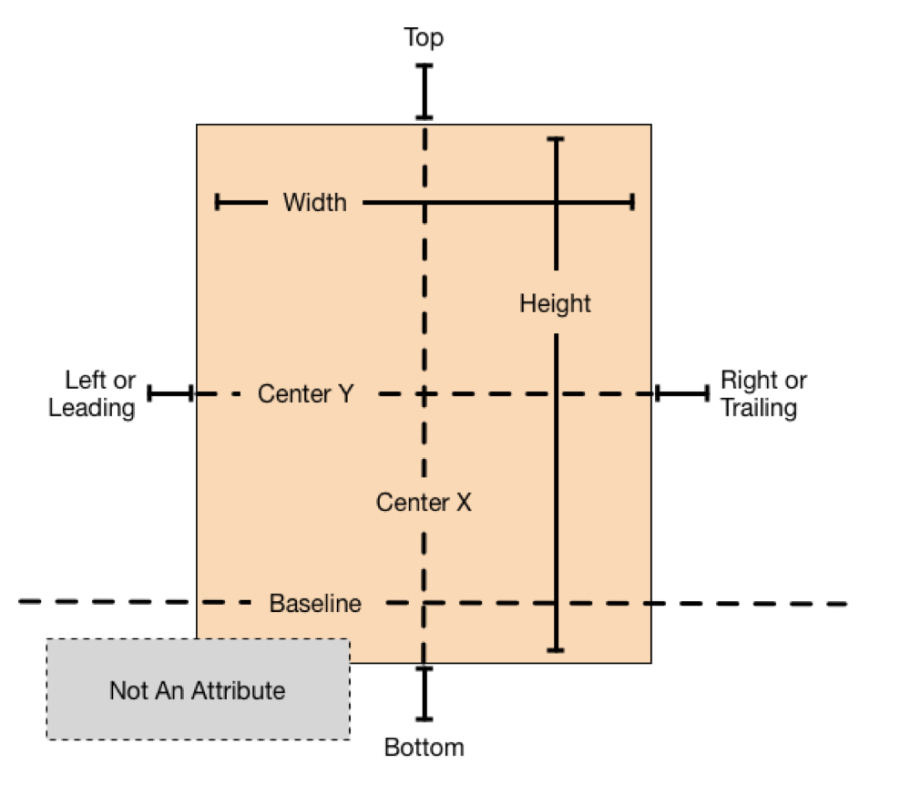
속성의 전체 목록은 NSLayoutAttribute enum을 참조하십시오.

NOTE

OS X와 iOS 모두 NSLayoutAttribute enum을 사용하지만 다소 다른부분이 있습니다. 속성 전체 목록을 확인하기 전에 찾고자하는 플랫폼의 문서를 보고 있는지 확인하세요.

방정식 예시(Sample Equations)

방정식에 사용할 수 있는 광범위한 매개변수 및 속성을 통해 다양한 유형의 제약 조건을 만들 수 있습니다. 서로 다른 View의 간격을 정의하고, edge를 정렬할 수 있으며, 상대적 크기를 정의하거나 종횡 비율을 정의할 수 있습니다. 하지만 모든 속성이 호환되는 것은 아닙니다.

속성은 크기 속성(예: height 및 width)과 위치 속성(예: leading, left 및 top)으로 나뉩니다. 크기 속성은 위치 표시 없이 항목의 크기를 지정하는 데 사용됩니다. 위치 속성은 항목의 상대적인 위치를 지정하는 데 사용됩니다. 그러나 항목의 크기에 대한 표시는 없습니다.

이러한 차이점을 염두에 두고 다음 규칙이 적용됩니다.

크기 속성을 위치 속성으로 제한할 수 없습니다.
위치 속성에 상수 값을 할당할 수 없습니다.
위치 속성에는 비식별 multiplier(1.0 이외의 값)를 사용할 수 없습니다.
위치 속성의 경우 horizontal 속성을 vertical 속성으로 제한할 수 없습니다.
위치 속성의 경우 leading 또는 trailing 속성을 left 또는 right 속성으로 제한할 수 없습니다

예를 들어 item의 top을 상수 값 20.0으로 설정하는 것은 추가 context가 없으면 의미가 없습니다. 항상 다른 item과 관련하여 항목의 위치 속성을 정의해야 합니다 (예: SuperView의 상단에서 20.0포인트 아래). 그러나 항목의 높이를 20.0으로 설정하는 것은 완벽하게 유효합니다. 자세한 내용은 Interpreting Values를 참조하세요.

목록 3-1은 다양한 공통 제약 조건에 대한 방정식 예시

NOTE

이 장의 모든 예제 방정식은 의사 코드(pseudocode)를 사용하여 표시됩니다. 실제 코드를 사용하여 실제 제약 조건을 보려면 Programmatically Creating Constraints 또는 Auto Layout Cookbook을 참조하십시오.

목록 3-1공통 제약 조건에 대한 샘플 방정식


swift
// Setting a constant height
View.height = 0.0 * NotAnAttribute + 40.0

// Setting a fixed distance between two buttons
Button_2.leading = 1.0 * Button_1.trailing + 8.0

// Aligning the leading edge of two buttons
Button_1.leading = 1.0 * Button_2.leading + 0.0

// Give two buttons the same width
Button_1.width = 1.0 * Button_2.width + 0.0

// Center a view in its superview
View.centerX = 1.0 * Superview.centerX + 0.0
View.centerY = 1.0 * Superview.centerY + 0.0

// Give a view a constant aspect ratio
View.height = 2.0 * View.width + 0.0

할당을 의미하는 것이 아니라 같음을 의미하는 것이다.(Equality, Not Assignment)

Note에 표시된 방정식은 값을 할당하는 것을 나타내는 것이 아니라 두 항이 같음을 나타냅니다. Auto Layout은 이러한 방정식을 풀 때 단순히 오른쪽의 값을 왼쪽에 할당하지 않습니다. 대신 관계를 참으로 만드는 attribute 1과 attribute 2 모두에 대한 값을 계산합니다. 이것은 우리가 종종 방정식의 항목을 자유롭게 재정렬할 수 있음을 의미합니다. 예를 들어 목록 3-2의 방정식은 Note의 해당 방정식과 동일합니다.

목록 3-2 역 방정식(Inverted equations)


swift
// Setting a fixed distance between two buttons
Button_1.trailing = 1.0 * Button_2.leading - 8.0

// Aligning the leading edge of two buttons
Button_2.leading = 1.0 * Button_1.leading + 0.0

// Give two buttons the same width
Button_2.width = 1.0 * Button.width + 0.0

// Center a view in its superview
Superview.centerX = 1.0 * View.centerX + 0.0
Superview.centerY = 1.0 * View.centerY + 0.0

// Give a view a constant aspect ratio
View.width = 0.5 * View.height + 0.0

NOTE

항목을 재정렬할 때 multiplier와 상수를 반전시켜야 합니다. 예를 들어 상수 8.0은 -8.0이 됩니다. multiplier 2.0은 0.5가 됩니다. 상수 0.0과 승수 1.0은 변경되지 않습니다.

오토 레이아웃이 동일한 문제를 해결하는 여러 가지 방법을 자주 제공한다는 것을 알게 될 것입니다. 이상적으로는 의도를 가장 명확하게 보여주는 것이 좋습니다. 그러나 개발자마다 정답은 다릅니다. 공통의 정답을 찾기 보단 일관성을 유지하는 것이 좋습니다. 일관적인 방식을 유지한다면 장기적으로 문제를 덜 경험하게 될 것입니다. 예를 들어 이 가이드에서는 다음과 같은 경험 법칙을 사용합니다.

multiplier는 분수보다 정수를 권장합니다.
상수는 양수를 음수보다 권장합니다.
가능하면 View는 layout 순서로 나타나야 합니다.

애매하지 않고 온전한 레이아웃 만들기(Creating Nonambiguous, Satisfiable Layouts)

오토 레이아웃을 사용할 때 목표는 가능한 정답이 하나만 있는 일련의 방정식을 사용하는 것입니다. 모호한 제약 조건에는 하나 이상의 솔루션이 있습니다. 조건이 충족되지 않은 제약 조건에는 유효한 솔루션이 없습니다.

일반적으로 제약 조건은 각 View의 크기와 위치를 모두 정의해야 합니다. SuperView의 크기가 이미 설정되어 있다고 가정하면(예: iOS에서 Scene의 루트 뷰) 모호하지 않고 온전한 레이아웃에는 차원당 View당 두 개의 제약 조건이 필요합니다(SuperView는 포함하지 않음). 그러나 사용하려는 제약 조건을 선택할 때 다양한 옵션이 있습니다. 예를 들어, 다음 세 가지 레이아웃은 모두 명확하고 온전한 레이아웃을 생성합니다(horizontal 제약 조건만 표시됨).

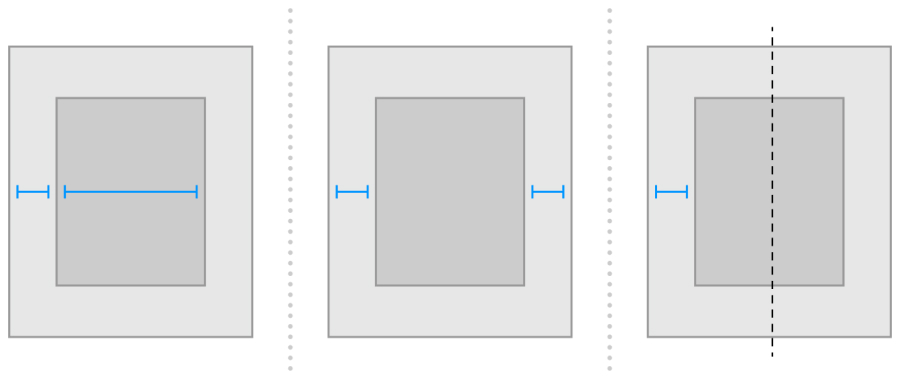
첫 번째 레이아웃은 SuperView의 leading edge를 기준으로 View의 leading edge를 제한합니다. 또한 View에 고정 width를 제공합니다. trailing 에지의 위치는 SuperView의 크기 및 기타 제약 조건을 기반으로 계산할 수 있습니다.
두 번째 레이아웃은 SuperView의 leading edge를 기준으로 View의 leading edge를 제한합니다. 또한 SuperView의 trailing 에지를 기준으로 View의 trailing 에지를 제한합니다. View의 width는 SuperView의 크기 및 기타 제약 조건을 기반으로 계산할 수 있습니다.
세 번째 레이아웃은 SuperView의 leading edge를 기준으로 View의 leading edge를 제한합니다. 또한 View와 SuperView를 가운데 정렬합니다. 그런 다음 SuperView의 크기 및 기타 제약 조건을 기반으로 width와 trailing edge의 위치를 계산할 수 있습니다.

각 레이아웃에는 하나의 View와 두 개의 horizontal 제약 조건이 있습니다. 각각의 경우에 제약 조건은 View의 width와 horizontal 위치를 모두 정의합니다. 즉, 모든 레이아웃이 horizontal axis를 따라 명확하고 온전한 레이아웃을 생성합니다. 그러나 이러한 레이아웃은 똑같이 유용하지 않습니다. SuperView의 width가 변경될 때 어떤 일이 발생하는지 고려하십시오.

첫 번째 레이아웃에서 View의 width는 변경되지 않습니다. 대부분의 경우 이것은 원하는 것이 아닙니다. 실제로 일반적으로 View에 일정한 크기를 할당하지 않아야 합니다. 오토 레이아웃은 환경에 동적으로 적응하는 레이아웃을 생성하도록 설계되었습니다. View에 고정된 크기를 제공하는 것은 레이아웃이 확정되어, 기능이 단락(더 이상 레이아웃을 계산하지 않음)되는 것입니다.

명확하지 않을 수 있지만 두 번째 및 세 번째 레이아웃은 동일한 동작을 생성합니다. 두 레이아웃 모두 SuperView의 width가 변경될 때 View와 해당 SuperView 사이에 고정된 여백을 유지합니다. 그러나 반드시 같지는 않습니다. 일반적으로 두 번째 예가 이해하기 쉽지만 특히 여러 항목을 가운데 정렬할 때 세 번째 예가 더 유용할 수 있습니다. 항상 그렇듯이 특정 레이아웃에 가장 적합한 방법을 선택하십시오.

이제 조금 더 복잡한 상황을 가정해 봅시다. iPhone에 두 개의 뷰를 나란히 표시하고 싶다고 상상해 보십시오. 당신은 그들이 모든면에 좋은 여백을 가지고 있고 항상 같은 너비를 가지고 있는지 확인하고 싶습니다. 또한 장치가 회전되어도 조건이 유지되어야 합니다.

다음 그림은 portrait 및 landscape 방향의 View를 보여줍니다.

그렇다면 이러한 제약 조건은 어떤 모습이어야 할까요? 다음 그림은 하나의 간단한 솔루션을 보여줍니다.

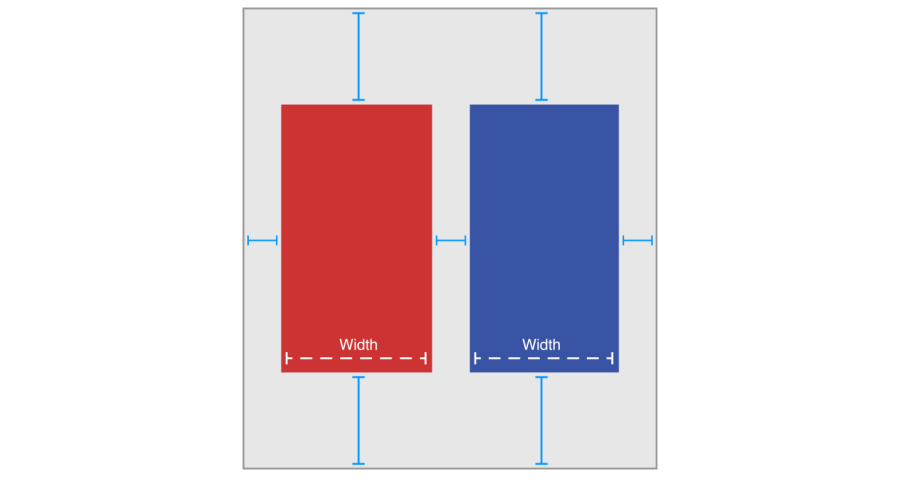
위의 솔루션은 다음 제약 조건을 사용합니다.


swift
// Vertical Constraints
Red.top = 1.0 * Superview.top + 20.0
Superview.bottom = 1.0 * Red.bottom + 20.0
Blue.top = 1.0 * Superview.top + 20.0
Superview.bottom = 1.0 * Blue.bottom + 20.0

// Horizontal Constraints
Red.leading = 1.0 * Superview.leading + 20.0
Blue.leading = 1.0 * Red.trailing + 8.0
Superview.trailing = 1.0 * Blue.trailing + 20.0
Red.width = 1.0 * Blue.width + 0.0

이전 경험 법칙에 따라 이 레이아웃에는 2개의 V,iew 4개의 horizontal 제약 조건 및 4개의 vertical 제약 조건이 있습니다. 이것이 완벽한 가이드는 아니지만 올바른 길을 가고 있다는 빠른 표시입니다. 더 중요한 것은 제약 조건이 두 View의 크기와 위치를 모두 고유하게 지정하여 명확하고 온전한 레이아웃을 생성한다는 것입니다. 이러한 제약 조건을 제거하면 레이아웃이 모호해집니다. 추가 제약 조건을 추가하면 충돌이 발생할 위험이 있습니다.

그러나 이것이 유일한 해결책은 아닙니다. 다음은 동등하게 유효한 접근 방식입니다.

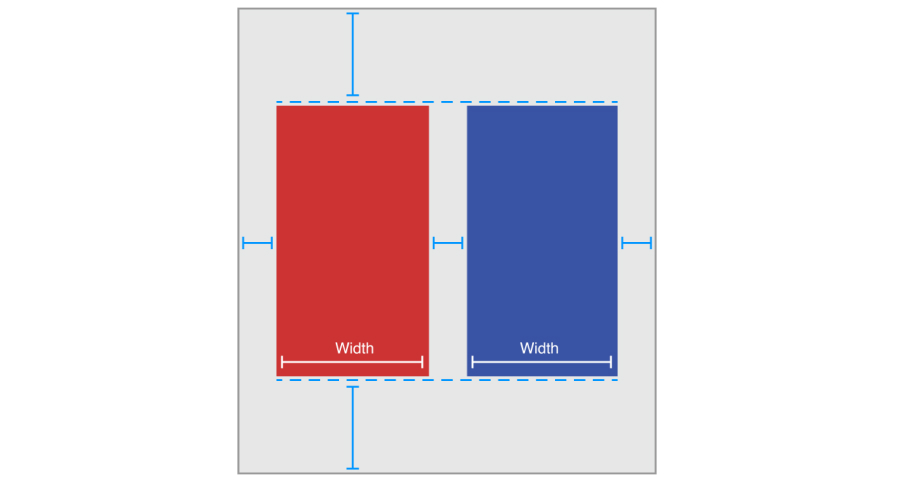
BlueView의 상단과 하단을 SuperView에 고정하는 대신 BlueView의 상단을 RedView의 상단과 정렬합니다. 마찬가지로 BlueView의 아래쪽을 RedView 상자의 아래쪽에 맞춥니다. 제약 조건은 다음과 같습니다.


swift
// Vertical Constraints
Red.top = 1.0 * Superview.top + 20.0
Superview.bottom = 1.0 * Red.bottom + 20.0
Red.top = 1.0 * Blue.top + 0.0
Red.bottom = 1.0 * Blue.bottom + 0.0

//Horizontal Constraints
Red.leading = 1.0 * Superview.leading + 20.0
Blue.leading = 1.0 * Red.trailing + 8.0
Superview.trailing = 1.0 * Blue.trailing + 20.0
Red.width = 1.0 * Blue.width + 0.0

예제에는 여전히 2개의 View 4개의 수평 horizontal 조건 및 4개의 vertical 제약 조건이 있습니다. 여전히 명확하고 온전한 레이아웃을 생성합니다.

무엇이 더 좋은 방법일까?

위 예시들은 모두 의도한 레이아웃을 생성합니다. 그런데 무엇이 더 좋은 방법일까요? 불행히도 한 접근 방식이 다른 접근 방식보다 엄격하게 우월하다는 것을 객관적으로 증명하는 것은 사실상 불가능합니다. 각각 고유한 강점과 약점이 있습니다. 첫 번째 솔루션은 View가 제거될 때 강점이 나타납니다. View 계층 구조에서 View를 제거하면 해당 View를 참조하는 모든 제약 조건도 제거됩니다. 따라서 RedView를 제거하면 BlueView에는 세 가지 제약 조건이 그대로 유지됩니다. 단일 제약 조건만 추가하면 유효한 레이아웃이 다시 생성됩니다. 두 번째 솔루션에서 RedView를 제거하면 BlueView에 단일 제약 조건만 남게 됩니다. 반면 첫 번째 솔루션에서 View의 상단과 하단을 정렬하려면 상단과 하단 제약 조건이 동일한 상수 값을 사용하는지 확인해야 합니다. 하나의 상수를 변경하면 다른 상수도 변경해야 합니다.